Hyperloop: riding sound’s density peak to exploit the drag equation
Super short version: if you ride along with a low enough frequency soundwave at the speed of sound, you can trade reduced incoming particle velocity for increased incoming particle density; the drag equation favors this heavily as it has both a density factor and a velocity squared factor; take this trade to an extreme with a high enough amplitude sound wave and you get nearly-adiabatic travel between point A and point B at the speed of sound
Hyperloop is Elon Musk’s proposed means of travel that could enable a trip between San Francisco and LA in 30 minutes (which would mean you travel at roughly the speed of sound). He is supposed to be revealing an “alpha” design in August. I think I have finally worked it out what it will be, and passengers should find themselves travelling at exactly the speed of sound.
The method I propose would enable extremely low drag (i.e. air resistance) at sea-level altitude without doing anything that has to affect the air across the whole loop (e.g. evacuating the entire tube or circulating the entire column of air). The key is a combination of a scaling property of the high-velocity drag equation and a clever way to exploit it by traveling within the density peak of an intense low-frequency sound wave.
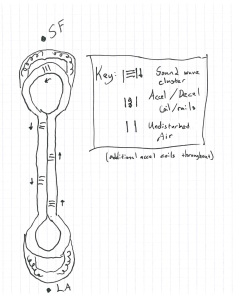
Hyperloop is mainly just a looping tube (with entry/exit accelerators/decelerators) that acts as a waveguide for these bursts of soundwaves:
The properties of sound waves get interesting when you view them from the reference frame of a vehicle embedded within, traveling in the direction of the wave at the speed of sound. The vehicle remains fixed on one point of the pressure wave as the wave propagates. Depending on the point along the wave you chose, air density and air velocity differ inversely, allowing net airflow to always remain the same (as required if you are to move through the air; sound waves themselves just jiggle air back and forth and don’t actually move it anywhere in the long run).
Traveling in the wave’s trough, a vehicle would face a sparse number of molecules whizzing by at high velocities, but riding the peak, the vehicle would only have to deal with a dense cloud of molecules slowly crawling by. The latter turns out to involve much less drag over the course of a hyperloop trip!
the high velocity drag equation, Fd = (½)P*(V^2) CdA
The force of drag increases proportionately as the square of the air velocity (v^2), but only linearly with air density (ρ)! If you double the density, you only double the drag, but if you instead double the velocity, you quadruple the drag. The drag equation is ultimately this way because incoming particles impart a momentum of only m*v on the craft but a kinetic energy of m*v^2. In the dense part of the wave there is a high potential energy, but low kinetic energy (with respect to the net velocity of the air). In the sparse part the potential energy has been converted into net velocity (temperature goes down and velocity goes up as the gas expands).
This in turn means that when traveling along with the sound wave, all the vehicle needs to do to minimize drag is stay on the wave peak–the area of highest density and lowest apparent velocity. And the higher the amplitude of the wave hyperloop manages to generate, the higher the density, the slower the apparent air velocity, and the lower the drag during the trip! Crank it up enough and you approach fully adiabatic travel.
So, in the launching area the vehicle reaches the speed of sound and is then ejected into the main loop at exactly the right time to be at the peak of a passing sound wave. All it then needs to do is use a low amount of force to fight the drag induced by the dense soup of slow, incoming air (slow from the vehicle’s reference frame) for around 30 minutes or so, and BAM! it has traveled from San Francisco to Los Angeles. That’s it; that’s hyperloop. You shouldn’t really need to read the rest.
But, I’ll quickly go over how this version of Hyperloop can meet the conditions hinted at by Elon Musk:
-
It lets you travel from LA to San Francisco in around 30 minutes
-
It is like a cross between a Concorde, a railgun, and an air-hockey table
-
It isn’t affected by earthquakes
-
It could use solar to be self-powering
-
It can store excess solar energy within the system itself
-
You can’t crash
It lets you travel from LA to San Francisco in around 30 minutes:
This is roughly the speed of sound; everything I’ve mentioned depends on moving at this speed.
It is like a cross between a Concorde,
Sonic-ish speeds and lots of noise?
…a railgun,
I think acceleration/deceleration will be done in a separate area from the main loop; if the vehicles were accelerated in the main tubes there would be the possibility of wave reflectance if a wave passed by before it was up to speed. Anyway, this could be done with a railgun or a coilgun; I suspect coilgun because that would also be an easy design to use for maintaining vehicle velocity with solar during the main stretches of the loop.
…and an air-hockey table
You could scoop in some of the dense air and blow it through air hockey holes at the bottom of the craft… If the pressure is high enough at the soundwave peak, you could design the craft to be neutrally buoyant (I think we’d be getting into shock wave territory by that point though).
It isn’t affected by earthquakes
I believe some fragile historic buildings have been anchored to a slab that rests atop a second slab anchored to the ground; in an earthquake the slabs just slide freely over each other and the structure doesn’t feel much force.
Same deal here; anchor each Hyperloop tube-support to a sliding slab.
It could use solar to be self-powering
PV solar would be used to power the rail/coilguns that maintain the vehicle’s speed in the low drag environment. Solar would also be used to create and maintain the sound wave; maybe it could use cheap thermal solar along with PV to create waves in the manner of a thermoacoustic engine.
It can store excess solar energy within the system itself
The waves travelling throughout the system would be the energy storage. Friction losses between air and the tube walls could be mitigated by just increasing the diameter of the tube: the perimeter grows proportional to the diameter, but the encircled air grows as the diameter squared. So that scales well. Lowering the wave frequency in the design could minimize losses as well by making the waves more and more adiabatic in nature.
You can’t crash
Famous last words…

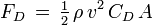

Recent Comments